Teachers' Domain - Digital Media for the Classroom and Professional Development
User: Preview
Animations and essays were created and written by Dr. Michael Gallis, the Pennsylvania State University.
Teachers who reviewed the collection were Patrick Callahan, Tara Clopper, and David R. McCachren. Instructional designer was Rucha Modak. Multimedia producer was Betsy Hutton. Director of Educational Services, Penn State Public Broadcasting is Dr. Babs Bengtson.
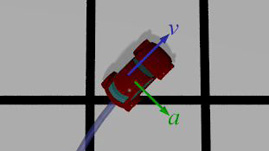
This overhead view of an animated car illustrates its velocity and acceleration as it starts up, moves in a straight line, and turns.
Velocity is one way we describe motion, and includes the notions of both speed and direction: going fast versus going slow, going east versus going north. Velocity is how position changes with time. Acceleration is how we describe the changes in velocity over time: speeding up, slowing down and changing direction are all examples of when acceleration occurs.
Knowing how to describe motion is an important first step in understanding the underlying physics that governs changes in motion. We see changes in motion all the time, as we go to work or school, participate in sports or even wander around our homes. If we never changed our own motion, we would never make it out of bed in the morning!
Velocity is one way we describe motion, and includes the notions of both speed and direction: going fast versus going slow, going east versus going north. Velocity is how position changes with time. Acceleration is how we describe the changes in velocity over time: speeding up, slowing down and changing direction are all examples of when acceleration occurs. As a result, velocity is to position as acceleration is to velocity, so we tend to use similar mathematics in describing these quantities.
We can model velocity and acceleration by imagining arrows whose size represents "how big" and which also point in the direction of their respective quantity. These arrows are a visual representation of what we call vectors. When a car starts from rest and accelerates straight down the road, the acceleration vector points forward while the velocity points forward and grows in length as the car speeds up. Once at a constant cruising speed and the acceleration has ceased, the acceleration vector “disappears” (acceleration is zero), while the velocity vector points straight ahead at a fixed size to represent a fixed speed.
Whenever the car speeds up without changing direction, the acceleration vector points straight ahead (relative to the front of the car), and the velocity vector grows longer. When the car slows down, the acceleration points in the opposite direction (towards the rear of the car) and the velocity vector shrinks in length. When a car turns at a constant speed, the acceleration points towards the side of the car in the direction the turn is being made. A sharper turn requires greater acceleration. The velocity vector always points towards the front (assuming we are not driving backwards down the highway!) so that it changes direction with the direction of motion of the car. As a result, when making turns at constant speed the acceleration and velocity are perpendicular! Generally motion is not limited to constant speed or direction; the acceleration vector provides us with information about changing speed as well as changing direction.
 Loading Standards
Loading Standards Teachers' Domain is proud to be a Pathways portal to the National Science Digital Library.
Teachers' Domain is proud to be a Pathways portal to the National Science Digital Library.
