Teachers' Domain - Digital Media for the Classroom and Professional Development
User: Preview
Animations and essays were created and written by Dr. Michael Gallis, the Pennsylvania State University.
Teachers who reviewed the collection were Patrick Callahan, Tara Clopper, and David R. McCachren. Instructional designer was Rucha Modak. Multimedia producer was Betsy Hutton. Director of Educational Services, Penn State Public Broadcasting is Dr. Babs Bengtson.
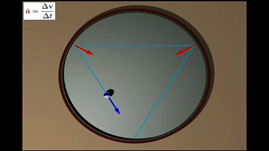
To try to understand the physics behind an object moving in a circle, we can consider an object whose motion follows the shape of a polygon. In this animation a ball bounces off the sides of the circle or polygon, and the number of sides double, until we get what appears to be a circle with a force on the ball that is constant in size and always directed towards the center.
How many sides does a circle have? One way of looking at a circle is as a series of regular polygons with ever increasing number of sides. Start by imagining an equilateral triangle (a three sided polygon). Adding a side results in a square. Adding another results in a pentagon. As we continue to add sides, notice that the polygon begins to take on the shape of a circle. One could say that a perfect circle is just an infinite-sided regular polygon. To try to understand the physics behind an object moving in a circle, we can consider an object whose motion follows the shape of a polygon.
Changes in motion are caused by forces as described by Newton’s Laws. Consider a pool ball rolling on an otherwise empty pool table: the speed of the ball is very nearly constant and the velocity is constant except when the ball bounces off the wall. On each bounce there is a “kick” or impulse on the ball that is directed perpendicular to the wall. Now imagine using a circular physics pool table, and set the ball so that its path is an equilateral triangle. When the ball comes to a corner of the triangle, it bounces off the wall. The “kick” from the wall is always directed towards the center of the table. Our “three sided circle” is created by the intermittent kick off the wall corresponding to a force directed towards the center of the table. When we double the number of sides of our polygon to six, the deflections of the ball’s path are half as big, but they occur twice as often, so that the size of the average force will be the same. We can continue to double the number of sides of the polygon until we get what appears to be a circle with a force on the ball that is constant in size and always directed towards the center.
We often hear the term centrifugal force is often misidentified as an “outward force” on an object going in a circle, when there is actually no force outward. The object is continuing a straight-line motion due to its inertia. When we feel pressed to the left in a car making a right hand turn, we are actually just experiencing the car moving out from underneath us to the right and the seats, seat belts and car door exert the necessary force to change our body’s motion so that we follow the circular path of the car. If we re-examine our circular pool table and remove a section of the wall, the ball would just go straight where there was no wall to deflect its path.
To learn more about the application of circular motion to amusement park physics, check out Centripetal Force: Roller Coaster Loops.
To learn more about the physics of circular motion, check out Circular Motion.
 Loading Standards
Loading Standards Teachers' Domain is proud to be a Pathways portal to the National Science Digital Library.
Teachers' Domain is proud to be a Pathways portal to the National Science Digital Library.
